FFT Peak 주파수 추정 방식 (이차 보간법, 가중평균법, parabolic inpterpolation, weighted average) 비교

FFT를 그냥 진행하면 Leakage(누설)가 발생한다. 누설이라는 용어보단 Leakage가 편해서 Leakage로 표현하겠다. 이는 우리가 흔히 FBIN이라고 하는 주파수 Resolution이 입력 신호와 맞지 않아 발생하는 흔한 현상이다. 이해를 돕기 위해서 부연하면 FBIN은 FFT의 X축의 간격이다.

이런 현상을 완화시키기 위해서 윈도우를 씌우기도 하지만 Leakage를 완전히 막지는 못한다. 따라서 정확한 Peak 주파수를 얻기 위해선 Peak 주파수 주변 신호를 활용해 정확도를 높이는 방식을 적용해 볼 수 있다.

여기서 소개할 방식은 2가지로 신호에서 흔히 사용되는 이차 보간법과 가중평균법이다. 결론적으로 주파수를 가변하며 FFT를 하고 FFT의 결과에서 2가지 방식을 통해 주파수를 다시 계산했다. 그리고 원래 입력 주파수와 계산된 주파수의 차이를 Error로 하여 결과에 Plot하는 코드를 작성했다.

코드는 OCTAVE로 작성되어서 MATLAB에서도 무난히 동작할 것이다.

코드 예제

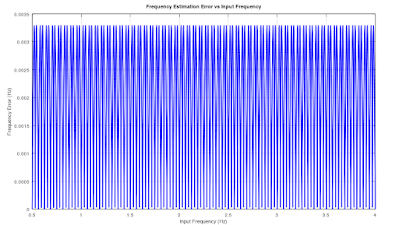
이차보간법 코드 (Parabolic Interpolation)

% Load the signal package

pkg load signal;

% Octave Script for Precise Peak Frequency Estimation Considering Windowing Effect

% Parameters

Fs = 128; % Sampling frequency

NFFT = 2048; % FFT points

freq_range = 0.5:0.0001:4; % Frequency range to test

errors = zeros(size(freq_range)); % Initialize error array

% Window function (Hann window)

window = hann(NFFT);

for i = 1:length(freq_range)

% Generate the signal with frequency freq_range(i)

f = freq_range(i);

t = (0:NFFT-1) / Fs;

signal = sin(2 * pi * f * t);

% Apply window

windowed_signal = signal .* window';

% FFT

X = abs(fft(windowed_signal, NFFT));

X = X(1:NFFT/2+1); % Only positive frequencies

% Find peak index

[~, k_peak] = max(X);

% Quadratic interpolation to find a more precise peak location

if k_peak > 1 && k_peak < NFFT/2

alpha = X(k_peak - 1);

beta = X(k_peak);

gamma = X(k_peak + 1);

% Parabolic interpolation formula to refine peak index

delta = 0.5 * (alpha - gamma) / (alpha - 2 * beta + gamma);

k_interp = k_peak + delta;

else

k_interp = k_peak; % No interpolation possible at boundaries

end

% Convert to frequency

f_interp = (k_interp - 1) * Fs / NFFT;

% Calculate error

errors(i) = abs(f - f_interp);

end

% Plotting the results

figure;

plot(freq_range, errors, 'b', 'LineWidth', 2);

xlabel('Input Frequency (Hz)');

ylabel('Frequency Error (Hz)');

title('Frequency Estimation Error vs Input Frequency');

grid on;

가중 평균법 코드 (Weighted Average)

% Load the signal package

pkg load signal;

% Octave Script for Precise Peak Frequency Estimation Using Amplitude Weights

% Parameters

Fs = 128; % Sampling frequency

NFFT = 2048; % FFT points

freq_range = 0.5:0.0001:4; % Frequency range to test

errors = zeros(size(freq_range)); % Initialize error array

% Window function (Hann window)

window = hann(NFFT);

for i = 1:length(freq_range)

% Generate the signal with frequency freq_range(i)

f = freq_range(i);

t = (0:NFFT-1) / Fs;

signal = sin(2 * pi * f * t);

% Apply window

windowed_signal = signal .* window';

% FFT

X = abs(fft(windowed_signal, NFFT));

X = X(1:NFFT/2+1); % Only positive frequencies

% Find peak index

[~, k_peak] = max(X);

% Weighted average using amplitude squared

if k_peak > 1 && k_peak < NFFT/2

Fm1 = (k_peak - 2) * Fs / NFFT;

F0 = (k_peak - 1) * Fs / NFFT;

Fp1 = k_peak * Fs / NFFT;

Am1 = X(k_peak - 1);

A0 = X(k_peak);

Ap1 = X(k_peak + 1);

% Weighted frequency estimation

f_estimated = (Fm1 * Am1^2 + F0 * A0^2 + Fp1 * Ap1^2) / (Am1^2 + A0^2 + Ap1^2);

else

% Edge case, use peak bin frequency

f_estimated = (k_peak - 1) * Fs / NFFT;

end

% Calculate error

errors(i) = abs(f - f_estimated);

end

% Plotting the results

figure;

plot(freq_range, errors, 'b', 'LineWidth', 2);

xlabel('Input Frequency (Hz)');

ylabel('Frequency Error (Hz)');

title('Frequency Estimation Error vs Input Frequency Using Amplitude Weights');

grid on;

코드 실행 결과

가중 평균 방식 (Weight Average)

MAX Error=1.84e-3 Hz, fbin=3.125e-2

Error 비율: 0.0589 (약 17.0배 감소)

이차 보간 방식 (Parabolic Interpolation)

MAX Error=3.30e-3 Hz, fbin=3.125e-2

Error 비율: 0.1055 (약 9.5배 감소)

비교 결과

결론적으로 두 방식 모두 주파수의 정확도를 높이는데 도움이 되는 것이 확인 되었다. 이차 보간 방식은 FFT 파형의 모양을 바탕으로 추정하는 반면 가중 평균은 신호의 세기를 바탕으로 추정하기 때문에 더 정확도가 높은 것으로 판단된다. 따라서 앞으로 가중 평균을 기본으로 알고리즘을 구현할 계획이다.

또한 윈도우에 따라 차이도 있는데, blackman: 4.96e-3, hann: 1.84e-3, hamming: 1.076e-3으로 hamming이 가장 정확도가 우수했다.

이 블로그 검색

추천 게시물